

Next: Future Improvements
Up: Real-Time Ray Tracing on
Previous: The Algorithm
The biggest challenge with this implementation was the limited memory
on the renderers---208 bits per processor. This limit, along with the
desire to have at least a 1280x1024 display (and thus allow object
positions anywhere in this range), limited the implementation
of the algorithm to integer arithmetic; fixed-point would have taken
too many additional bits. Fixed-point is used at one
point, as noted below, but the ray parametric parameters, the model
description, and most intermediate values are kept as 12 or 24 bit
integers.
With most integers being on the order of 500, or 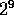 , problems arose
when calculating parts of the intersection formula. Namely, the
coefficients of the quadratic equation were on the order of the
squares of the integers, or
, problems arose
when calculating parts of the intersection formula. Namely, the
coefficients of the quadratic equation were on the order of the
squares of the integers, or 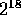 , and they themselves are squared
in the determinant of the quadratic formula, to yield numbers on the
order of
, and they themselves are squared
in the determinant of the quadratic formula, to yield numbers on the
order of 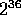 . The square root function needs an equal number of bit
for the input, the output, and some temporary space, so well over half
the the memory needs to be free just for the square root operation!
. The square root function needs an equal number of bit
for the input, the output, and some temporary space, so well over half
the the memory needs to be free just for the square root operation!
This problem led to the use of the Backing Store. The ray, which is
kept in six 12-bit integers, is swapped out to the Backing Store after
the coefficients of the quadratic equation are calculated. It
stays there until the parametric value T is calculated, whereupon
it is swapped back in and the intersection point is found.
The Backing Store is used a few other times to save important values
while their space is used for temporary variables.
To increase interactivity, the scene is rendered at one-quarter the
resolution (640x512) while the joystick is active; when the joystick
stops, the full resolution (1280x1024) is rendered.
Although the original idea was to use fixed-point for all variables,
some problems arose with the calculation of the parametric value T.
When the normal of the sphere is calculated, 12 bits are used to
store each of the normal's components, and the normal is simply
kept as the length of the sphere's radius. This yields a normal which
has length on the order of 200. When such a ray is intersected
with another sphere which is on the order of 400 units away, the
parametric value T truncates to 0, 1, or 2. To fix this, an additional
6 bits were added to the right of T's binary point, which significantly
helped the accuracy of the reflections. This bias is removed after
the value is plugged back into the ray.


Next: Future Improvements
Up: Real-Time Ray Tracing on
Previous: The Algorithm
Lawrence Kesteloot
Tue Jan 24 16:36:27 EST 1995
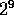 , problems arose
when calculating parts of the intersection formula. Namely, the
coefficients of the quadratic equation were on the order of the
squares of the integers, or
, problems arose
when calculating parts of the intersection formula. Namely, the
coefficients of the quadratic equation were on the order of the
squares of the integers, or 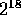 , and they themselves are squared
in the determinant of the quadratic formula, to yield numbers on the
order of
, and they themselves are squared
in the determinant of the quadratic formula, to yield numbers on the
order of 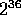 . The square root function needs an equal number of bit
for the input, the output, and some temporary space, so well over half
the the memory needs to be free just for the square root operation!
. The square root function needs an equal number of bit
for the input, the output, and some temporary space, so well over half
the the memory needs to be free just for the square root operation!