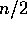If we want consensus to be possible without changing the system conditions, then we must change the definition of ``consensus''. Instead of requiring guarenteed consensus in finite time, we may want to have consensus in finite time with probability 1. In other words, there is a chance that the algorithm will be indefinitely delayed, but the probability of this happening is 0.
Bracha and Toueg [3] described algorithms for both fail-stop and Byzantine failures which, if n > 2t and n > 3t respectively, led to consensus with probability 1. Their algorithm is probabilistic but does not incorporate randomization, as is done in other algorithms which have finite-time consensus with probability 1 [1].
For the fail-stop resilient algorithm, the key idea is that if there are n processes, t of which may be expected to be faulty, then a process can never expect more than n-t acknowledgements from a broadcast. Each process then broadcasts its value and waits for n-t answers. The problem now is to make sure that whatever decision made on those n-t answers is the same as that made by another process, whose n-t answers may have come from a different set of processes (since not all t processes may be faulty).
The algorithm proceeds in phases. Each process broadcasts its
preferred value and the number of processes it has seen which
also have this as their preferred value. (The latter number,
the cardinality, is initially 1.) At each round, each
process receives n-t answers, each with a preferred value
and cardinality. The processes then change their
preferred value according to which value was preferred most
by other processes. This continues roughly like this until
a process, in a single phase, receives t messages of a single
value each with at least cardinality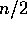 
, a which point it
knows that the algorithm will decide on that value in the next
two phases and it can stop (but not before broadcasting enough
messages for the next two phases).
Essentially, as the number of phases goes to infinity, the probability that consensus has not yet been reached goes to zero. Consensus with probability 1, although not as satisfying as guarenteed termination, is reasonable for most real systems.