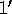 .
.
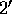 .
.
With oral messages, if one-third or more of the generals are traitorous, then no consensus is possible. Let us start by formalizing what we want from a consensus algorithm. We want all loyal generals to come to a concensus on a boolean value. If each general could create a list of what he thinks all the generals (including himself) want to do, then he could simply run a function on that list, say taking a majority, and the output of this ``majority'' function would be his decided value.
Therefore we are now faced with the problem of having to make sure that every general gets the exact same list, so that every general can run the same ``majority'' function on his list and come up with the same value, thus coming to a concensus.
We would like our Byzantine Agreement algorithm to satisfy two conditions:
We can simplify the model a bit. It is easy to see that if we solve the problem for one sender general and n-1 receiver generals, then we have solved it for n senders by simply running the one-sender algorithm n times. So as to not confuse the two models, we will speak of a commander sending orders to his n-1 lieutenants. Any lieutenant may be traitorous, and the commander himself may be traitorous. We rewrite our conditions as follows:
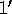 .
.
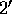 .
.
To get an intuitive feel for the problem, consider one commander and
two lieutenants, and one of the three is a traitor. If the commander
is traitorous, he can send a ``0'' to one lieutenant and a ``1'' to
the other. Since this would violate condition 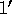 , our algorithm must
do more. The obvious next step is to have the lieutenants compare orders to
make sure the commander is not traitorous. Each lieutenant therefore
sends his received value to the other lieutenant.
, our algorithm must
do more. The obvious next step is to have the lieutenants compare orders to
make sure the commander is not traitorous. Each lieutenant therefore
sends his received value to the other lieutenant.
Let's look at it from lieutenant #1's point of view in two situations.
In the first, lieutenant #2 is a traitor and lieutenant #1 gets a
``0'' directly from the commander and
a ``The commander said `1','' from lieutenant #2.
In the second, the commander is a traitor
and lieutenant #1 gets a ``0'' directly from the commander and
a ``The commander said `1','' from lieutenant #2.
These two situations look the same to lieutenant #1. In the first
situation, according to condition 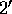 , he must choose the value ``0''.
Since the two situations look alike to him, he will also
choose ``0'' in the second situation. But in this second situation,
lieutenant #2 will choose ``1'' (by symmetry), thus violating
condition
, he must choose the value ``0''.
Since the two situations look alike to him, he will also
choose ``0'' in the second situation. But in this second situation,
lieutenant #2 will choose ``1'' (by symmetry), thus violating
condition 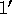 .
.
In fact, no amount of communication among the three people will allow the loyal lieutenant(s) to satisfy both conditions. Let us add one more lieutenant, but still only one of the four people is a traitor. In this new situation, less than one-third of the participants are traitors. Each lieutenant now gets three messages: one from the commander, and two from the other lieutenants. Since they are deciding on a binary value, then at least two of these messages will be the same, and the lieutenant can pick that value. To show that this value satisfies both conditions, we can do a case analysis.
If the commander is traitorous, he can send one value to one lieutentant
and the other value to the other two. When the lieutenants exchange
messages, they will each get the same list of three messages (since
they are all loyal), and will agree on the same value. (Remember that
condition 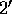 does not apply in this case.) If the commander is
loyal, then the two loyal lieutenants will get the true order and
can exchange it to confirm that theirs is the actual order. Even
if the traitorous lieutenant lies about the received order, he cannot
foil the other two since they will have a two-thirds majority on
the true order.
does not apply in this case.) If the commander is
loyal, then the two loyal lieutenants will get the true order and
can exchange it to confirm that theirs is the actual order. Even
if the traitorous lieutenant lies about the received order, he cannot
foil the other two since they will have a two-thirds majority on
the true order.
If there are t traitors, then there must be at least n=3t+1
loyalists. This was shown in the above situation and is easily
extended to any number of traitors. If t traitors are anticipated,
then t+1 rounds of information are exchanged. The first round has
the format, ``Here is my vote,'' and the second round has
the format, ``General 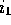 said x,'' and the third round has
the format, ``General
said x,'' and the third round has
the format, ``General 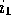 said that general
said that general 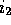 said x,'' and
so on. There is a total of
said x,'' and
so on. There is a total of 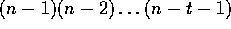 messages
exchanged.
messages
exchanged.
Yet, this limitation of having fewer than one-third of the generals be traitorous is bothersome; we would like to develop a system which is resilient to any number of traitors. We can achieve this with written messages.