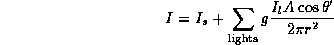
The above algorithm illuminates surface points for first-generation rays using point sampling, and is therefore subject to the usual aliasing artifacts. This is not very noticeable when the surface point is not in direct view of a light source because the intensities in the cells have low variance. Surface points that are in direct view of light sources, however, are likely to receive the majority of their intensity from the light source. Cells mapped to lights may be several dozen times brighter than cells mapped to non-emitting surfaces, and sampling differences between neighboring screen pixels can result in noticeable noise in the image.
Since most of the noise comes from sampling the light source, we can replace the area under the integral curve that corresponds to the lights with an analytical estimate:
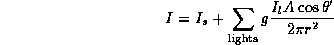
where 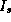 is the average of the
hemisphere without the lights' contributions, g is a geometric term
representing visibility,
is the average of the
hemisphere without the lights' contributions, g is a geometric term
representing visibility, 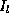 and A are the intensity and area of the
light source,
and A are the intensity and area of the
light source, 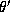 is the angle between the ray to the light source
and the light's normal vector, and r is the distance to the light.
(Notice that here we do use the geometric factors because the ray is not
random or evenly distributed across the hemisphere but rather aimed
directly at the light source.) Distribution ray-tracing is used here
to simulate penumbras, with 10 rays shot to each light. Removing the
light's contribution to the hemisphere is implemented by clipping each
cell's intensity to 1, with the assumption that most non-emitting surfaces
would contribute less and most lights would contribute more. The resulting
hemisphere is now acting as a better approximation to the tradition
constant ambient term.
is the angle between the ray to the light source
and the light's normal vector, and r is the distance to the light.
(Notice that here we do use the geometric factors because the ray is not
random or evenly distributed across the hemisphere but rather aimed
directly at the light source.) Distribution ray-tracing is used here
to simulate penumbras, with 10 rays shot to each light. Removing the
light's contribution to the hemisphere is implemented by clipping each
cell's intensity to 1, with the assumption that most non-emitting surfaces
would contribute less and most lights would contribute more. The resulting
hemisphere is now acting as a better approximation to the tradition
constant ambient term.