Female Fraction
Puzzle: There’s a certain country where everybody wants to have a son. Therefore each couple keeps having children until they have a boy; then they stop. What fraction of the population is female?
To be clear, we’re not asking, “What’s the average number of females in a family?” This is not asking per family. It’s asking, in the whole country, what’s the fraction of females to persons?
And since any specific instance of a country will have an unknown fraction (because of statistical variance), we’re really asking, “What is the expected fraction.” If you had a million universes, and computed the fraction of females to persons in each, and averaged the answers, what would you get?
Hint: Consider a one-family country.
Answer: Uh, it’s complicated.
Solution:
There are two ways to interpret this question:
- If you start with N couples, and they each follow the above algorithm and stop, what is the expected fraction of total girls to total children?
- If you have a population that follows the above algorithm generation after generation, what is the expected fraction of females to persons long-term?
For both interpretations the math sounds like it’d be pretty hard, but the easy answer is to observe that, regardless of parents’ wishes, half of all children born are girls, so half the population will be female. That’s the answer you’re supposed to give: 50%.
For the first interpretation, if you simulate it, you don’t get 50%. The answer depends on the number of families, and the more families there are in the country, the closer the answer approaches 50%, but it starts out pretty low when you have one family (around 31%). With four families you get up to around 44%.
Why is that? Well, the answer is that the parents stop when they have a son.
As an intuition pump, consider a country with only one family. In half the universes, they have a son and stop. The fraction is zero for half the universes. So the average will definitely be below 50% because in the other half the answer isn’t 100%! In no universe is the answer 100%, since each family has exactly one boy. The average of those percentages will be around 31%.
Here’s a graph showing the percent of girls given the number of families in the country:
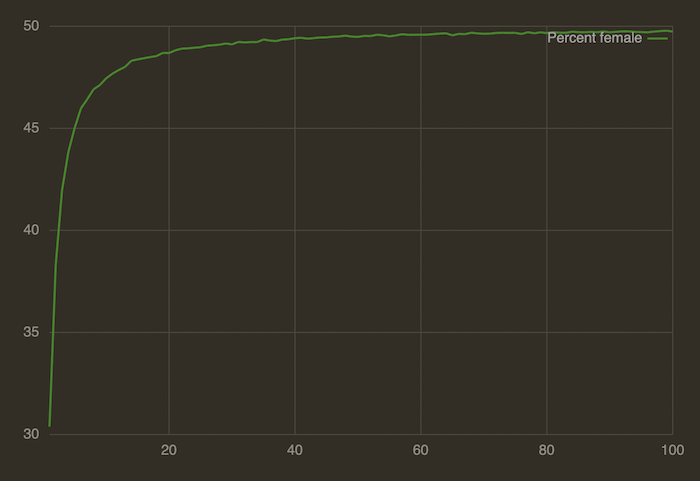
For the second interpretation, if you simulate it, the answer is also not 50%. That’s because each couple has on average 2 children, and that’s below the replacement rate of 2.1, so the population goes extinct pretty quickly. Before it goes extinct, the fraction dances around 50%, but it’s not possible to use that in an average over many universes. The answer here is undefined.
(The replacement rate is above 2 because you’ll never have exactly 50% adult females, so some people will die without finding a mate.)
The Python scripts in this repo run some simulations. Run female_fraction.py to get the one-generation simulation and long_term.py to get the steady state result.
References: