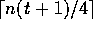 messages are necessary for
such an algorithm, where
n is the number of processes and t is the number of expected
faulty processes. With written messages, an average of
messages are necessary for
such an algorithm, where
n is the number of processes and t is the number of expected
faulty processes. With written messages, an average of
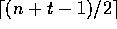 messages are necessary, which is
considerably better.
messages are necessary, which is
considerably better.
The Byzantine Generals Problem is a paradigm for distributed processes, some of which may be faulty. It might be fair to assume that most of the time, all processes will be correct (i.e., not faulty). An easy way to reduce the number of messages sent in a Byzantine Agreement algorithm would be to not run the algorithm at all if all of the processes are correct. We should then develop a Fault Detection algorithm which we run first, which would be weaker than the Byzantine Agreement algorithm. Specifically, either all processes are correct and they should come to a concensus, or at least one should detect the presence of a faulty process. Once a faulty process is detected, then the full-blown Byzantine Agreement algorithm can be run.
Hadzilacos and Halpern [10] showed that with oral messages,
an average of 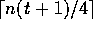 messages are necessary for
such an algorithm, where
n is the number of processes and t is the number of expected
faulty processes. With written messages, an average of
messages are necessary for
such an algorithm, where
n is the number of processes and t is the number of expected
faulty processes. With written messages, an average of
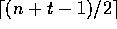 messages are necessary, which is
considerably better.
messages are necessary, which is
considerably better.
Instead of considering the number of messages, we could consider
the number of rounds. An algorithm
which tolerates t faulty processes must run at least t+1
rounds in worse-case execution; however, if the actual number
of faults f is less
than t, then there may be a way for the algorithm to terminate
earlier. This is referred to as early stopping, and
was described by Dolev et al. in [8]. They show
that if only fail-stop failures are allowed, then the minimum
number of rounds is 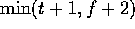 , and they present an algorithm
that achieves this bound. Since Byzantine failures are not
considered, this result is somewhat weaker, but possibly useful in
some systems where crashes are guarenteed to be the only faults.
, and they present an algorithm
that achieves this bound. Since Byzantine failures are not
considered, this result is somewhat weaker, but possibly useful in
some systems where crashes are guarenteed to be the only faults.
Another approach is to use non-determinancy (i.e., probability).
In [2],
Bracha presents a non-deterministic algorithm with an expected
number of rounds of 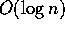 , as long as
, as long as 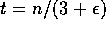 for oral messages or
for oral messages or 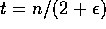 for written messages.
(The technique was later modified to yield a protocol with
for written messages.
(The technique was later modified to yield a protocol with
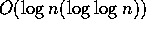 expected rounds.)
expected rounds.)
The key is to use other Byzantine Agreement algorithms which have the
following propreties: If t (number of faulty processes)
is 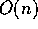 then the algorithm is
expenential in n, but if t is
then the algorithm is
expenential in n, but if t is 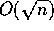 then the expected
number of rounds is constant. (There are several such algorithms, and
our meta-algorithm will work with any ``plug-in'' algorithm with
the above propreties.) If we can convert a system of
n processes and
then the expected
number of rounds is constant. (There are several such algorithms, and
our meta-algorithm will work with any ``plug-in'' algorithm with
the above propreties.) If we can convert a system of
n processes and 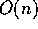 faulty processes into one with
m processes and
faulty processes into one with
m processes and 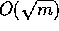 faulty processes, then we
can solve this new problem in constant time, leaving us only with
the time to translate one system into the other.
faulty processes, then we
can solve this new problem in constant time, leaving us only with
the time to translate one system into the other.
Bracha shows that if we choose 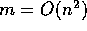 and have each of
these m processes be compound processes of
and have each of
these m processes be compound processes of 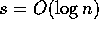 actual processes (each of which may be in several compound
processes), then we can choose the compound processes
in such a way that at most
actual processes (each of which may be in several compound
processes), then we can choose the compound processes
in such a way that at most 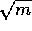 of them are faulty. A standard
of them are faulty. A standard
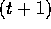 -round Byzantine Agreement protocol can be run in each of
the m compound processes (with an expected
-round Byzantine Agreement protocol can be run in each of
the m compound processes (with an expected  number
of rounds), and the result can be run on the m compound processes,
with an expected constant number of rounds. This yields a total
expected number of rounds of
number
of rounds), and the result can be run on the m compound processes,
with an expected constant number of rounds. This yields a total
expected number of rounds of 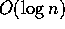 .
.