 .
.
The original Byzantine Generals problem as stated by Lamport et al. [12] did not specify that all processes had to decide on a value simultaneously, although the algorithm given in [12] had that proprety. In [11], Halpern et al. discuss the possibility of an algorithm in which the processes can decide independently and possibly earlier. This is called Eventual Byzantine Agreement, to differentiate it from Simultaneous Byzantine Agreement.
Their results are based on a technique called continual common
knowledge, which is a variant of common knowledge, i.e., the final result
of Simultaneous Byzantine Agreement. The key is that at some point
in the algorithm, some processor may have enough information to
realize that the algorithm will eventually decide on a particular
value. In other words, if common knowledge is that ``Everyone knows
that everyone knows that ... x,'' then eventual common knowledge
is that ``Everyone will know that everyone will know that ... x.''
It turns out that eventual common knowledge is too weak to solve the
problem (because of the way Byzantine Agreement is done), so continual
common knowledge (what everyone knows at any point in time) is used instead.
They give a construction which can translate any Eventual Byzantine Agreement
protocol P into an optimal protocol 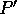 .
.