 of each other. Notice that if
of each other. Notice that if 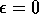 then it is equivalent
to the consensus problem with real values.
then it is equivalent
to the consensus problem with real values.
The topic of approximate agreement is not strictly a problem
of consensus, but is related and worth mentioning. We can
modify the Byzantine Generals Problem so that each process
inputs a real value rather than a binary value, and all processes
must eventually decide on real values which are within  of each other. Notice that if
of each other. Notice that if 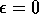 then it is equivalent
to the consensus problem with real values.
then it is equivalent
to the consensus problem with real values.
An algorithm described by Dolev et al. [7] works by
successive approximation. That is, every round gets closer to
the goal with a guarenteed convergence rate. The most interesting
part of this algorithm is that it works both in synchronous and
asynchronous systems (with 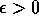 ).
The conditions are similar to that of
the consensus problem: all correct processes eventually halt
with output values within
).
The conditions are similar to that of
the consensus problem: all correct processes eventually halt
with output values within  of each other, and all
decided values are within the range of input values of all
correct processes. For synchronous systems, the convergence rate
depends on the ratio between the number of faulty processes
and the total number of processes. Convergence is guarenteed
when n > 3t. For asynchronous systems, convergence
is guarenteed when n > 5t.
of each other, and all
decided values are within the range of input values of all
correct processes. For synchronous systems, the convergence rate
depends on the ratio between the number of faulty processes
and the total number of processes. Convergence is guarenteed
when n > 3t. For asynchronous systems, convergence
is guarenteed when n > 5t.
The synchronous algorithm basically works as follows. Each
process sends its value to every other process. If a faulty
process does not send a value, then some default value, say 0,
is chosen. Each process then runs the function 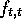 on
the n real values. Roughly speaking, the function f is chosen so as to
eliminate the lowest and highest t values from the list and
take the average of the rest;
the faulty processes are thus unable to affect the convergence
of the values. To show that it is necessary to have n > 3t,
assume n=3t. If all t faulty processes
send a very high value to correct process p and a very
low value to correct process q, then p and q will be taking
their averages on two completely different sets of numbers, and
they will not converge. However, if n=3t+1, then p and q
will have one overlapping value at their median, and will (very
slowly) converge towards each other.
on
the n real values. Roughly speaking, the function f is chosen so as to
eliminate the lowest and highest t values from the list and
take the average of the rest;
the faulty processes are thus unable to affect the convergence
of the values. To show that it is necessary to have n > 3t,
assume n=3t. If all t faulty processes
send a very high value to correct process p and a very
low value to correct process q, then p and q will be taking
their averages on two completely different sets of numbers, and
they will not converge. However, if n=3t+1, then p and q
will have one overlapping value at their median, and will (very
slowly) converge towards each other.
The asynchronous algorithm is the same as above, except that
each process only waits for n-t messages, does not choose
a default value, and runs the function 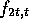 on the
list. It is interesting to note that although exact
consensus in a totally asynchronous system is impossible,
on the
list. It is interesting to note that although exact
consensus in a totally asynchronous system is impossible,
 can be chosen to be arbitrarily small to get
as close to consensus as desired.
can be chosen to be arbitrarily small to get
as close to consensus as desired.